数组
二分查找
function search(nums: number[], target: number): number {
let mid: number, left: number = 0, right: number = nums.length - 1;
while (left <= right) {
// 位运算 + 防止大数溢出
mid = left + ((right - left) >> 1);
if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
return mid;
}
}
return -1;
};
双指针 快慢指针 移除元素
暴力解法(我的想法) :
遍历数组 将所有等于要移除元素赋值为-1 然后再进行倒序排列即可 时间复杂度O(nlogn)
function removeElement(nums: number[], val: number): number {
let len:number = nums.length
let cnt:number = 0
for(let i = 0;i < len;i++){
if(nums[i] === val){
cnt++
nums[i] = -1
}
}
nums.sort((a,b)=> b-a)
return len - cnt
};快慢指针
通过一个快指针和慢指针在一个for循环下完成两个for循环的工作 时间复杂度O(n)
定义快慢指针
- 快指针:寻找新数组的元素 ,新数组就是不含有目标元素的数组
- 慢指针:指向更新 新数组下标的位置
function removeElement(nums: number[], val: number): number {
let slowIndex: number = 0, fastIndex: number = 0;
while (fastIndex < nums.length) {
if (nums[fastIndex] !== val) {
nums[slowIndex++] = nums[fastIndex];
}
fastIndex++;
}
return slowIndex;
};示意图
https://pic.leetcode-cn.com/1619009113-SlyHyv-008eGmZEly1gntrds6r59g30du09mnpd.gif
双指针 有序数组的平方
数组其实是有序的, 只不过负数平方之后可能成为最大数了
数组平方的最大值就在数组的两端,不是最左边就是最右边,不可能是中间
此时可以考虑双指针法了,i指向其实位置,j指向终止位置
定义一个新数组result,和A数组一样的大小,让k指向result数组终止位置
如果A[i] * A[i] < A[j] * A[j] 那么result[k–] = A[j] * A[j];
如果A[i] * A[i] >= A[j] * A[j] 那么result[k–] = A[i] * A[i];
示意图
function sortedSquares(nums: number[]): number[] {
let i = 0;
let j = nums.length - 1;
let result = new Array(nums.length); // 直接创建定长数组
for (let k = nums.length - 1; k >= 0; k--) {
const leftSquare = nums[i] * nums[i];
const rightSquare = nums[j] * nums[j];
if (leftSquare > rightSquare) {
result[k] = leftSquare;
i++;
} else {
result[k] = rightSquare;
j--;
}
}
return result;
}滑动窗口 双指针 长度最小的子数组
暴力解法 —> 超时了! 时间复杂度O(n*n)
function minSubArrayLen(target: number, nums: number[]): number {
let subLength = 0 //子数组长度
let result = 1e10 //最后结果
let sum = 0 //子数组总和
for(let i=0 ;i<nums.length;i++){
sum = 0
for(let j =i;j<nums.length;j++){
sum += nums[j]
if(sum>=target){
subLength = j - i + 1
break //发现即终止 再继续下去已经没有必要
}
}
result = result > subLength ? subLength : result
}
return result ? result : 0
}滑动窗口 时间复杂度O(n)
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果
在暴力解法中,是一个for循环滑动窗口的起始位置,一个for循环为滑动窗口的终止位置,用两个for循环 完成了一个不断搜索区间的过程
那么滑动窗口如何用一个for循环来完成这个操作呢
首先要思考 如果用一个for循环,那么应该表示 滑动窗口的起始位置,还是终止位置
如果只用一个for循环来表示 滑动窗口的起始位置,那么如何遍历剩下的终止位置?
此时难免再次陷入 暴力解法的怪圈
所以 只用一个for循环,那么这个循环的索引,一定是表示 滑动窗口的终止位置
示意图
function minSubArrayLen(target: number, nums: number[]): number {
let left:number = 0
let sum:number = 0
let res = Infinity
for(let right = 0;right<nums.length;right++){
sum+=nums[right]
while(sum>=target){
res = Math.min(res,right - left + 1)
sum -= nums[left++]
}
}
return res === Infinity ? 0 : res
}注意!
不要以为for里放一个while就以为是O(n^2)啊, 主要是看每一个元素被操作的次数,每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被操作两次,所以时间复杂度是 2 × n 也就是O(n)
双重循环 螺旋矩阵II
坚持循环不变量原则
模拟顺时针画矩阵的过程:
- 填充上行从左到右
- 填充右列从上到下
- 填充下行从右到左
- 填充左列从下到上

这里每一种颜色,代表一条边,我们遍历的长度,可以看出每一个拐角处的处理规则,拐角处让给新的一条边来继续画
function generateMatrix(n: number): number[][] {
let loopNum: number = Math.floor(n / 2);//右 -> 下 -> 左 -> 上一个循环的循环次数
const resArr: number[][] = new Array(n).fill(1).map(i => new Array(n));//创建二维数组
let chunkNum: number = n - 1; //每一个移动方向分块处理个数
//一个循环的起始位置
let startX: number = 0;
let startY: number = 0;
let value: number = 1;
let x: number, y: number;
while (loopNum--) {
x = startX;
y = startY;
while (x < startX + chunkNum) {
resArr[y][x] = value;
x++;
value++;
}
while (y < startY + chunkNum) {
resArr[y][x] = value;
y++;
value++;
}
while (x > startX) {
resArr[y][x] = value;
x--;
value++;
}
while (y > startY) {
resArr[y][x] = value;
y--;
value++;
}
startX++;
startY++;
chunkNum -= 2;
}
//单独处理中间的数字
if (n % 2 === 1) {
resArr[startX][startY] = value;
}
return resArr;
};
路径模拟 方向变换
可以模拟螺旋矩阵的路径。初始位置是矩阵的左上角,初始方向是向右,当路径超出界限或者进入之前访问过的位置时,顺时针旋转,进入下一个方向
判断路径是否进入之前访问过的位置需要使用一个与输入矩阵大小相同的辅助矩阵 visited,其中的每个元素表示该位置是否被访问过。当一个元素被访问时,将 visited 中的对应位置的元素设为已访问
如何判断路径是否结束?由于矩阵中的每个元素都被访问一次,因此路径的长度即为矩阵中的元素数量,当路径的长度达到矩阵中的元素数量时即为完整路径,将该路径返回
代码注释很清晰!
function spiralOrder(matrix: number[][]): number[] {
//特殊情况处理
if (!matrix.length || !matrix[0].length) {
return []
}
const rows: number = matrix.length //矩阵行数
const columns: number = matrix[0].length//矩阵列数
//辅助矩阵 visited,其中的每个元素表示该位置是否被访问过
const visited: boolean[][] = new Array(rows).fill(false).map(() => new Array(columns).fill(false))
const total: number = rows * columns //矩阵元素总数
const order: number[] = new Array(total).fill(0)//结果数组
let directionIndex: number = 0//路径方向
let row: number = 0
let column: number = 0
//各个方向路径对应的横纵坐标变化情况
const directions: [number, number][] = [[0, 1], [1, 0], [0, -1], [-1, 0]]
for (let i = 0; i < total; i++) {
order[i] = matrix[row][column]
visited[row][column] = true //已访问
//在当前移动路径情况下的下一行 与 下一列 用于后续判断是否越界/改变方向
const nextRow: number = row + directions[directionIndex][0]
const nextColumn: number = column + directions[directionIndex][1]
if (nextRow < 0 || nextRow >= rows ||
nextColumn < 0 || nextColumn >= columns ||
visited[nextRow][nextColumn]) {
directionIndex = (directionIndex + 1) % 4
}
//当前路径的下一行 下一列
row += directions[directionIndex][0]
column += directions[directionIndex][1]
}
return order
}前缀和 区间和
题目链接
https://kamacoder.com/problempage.php?pid=1070
普通做法会超时! 要使用前缀和!
前缀和的思想是重复利用计算过的子数组之和,从而降低区间查询需要累加计算的次数
前缀和 在涉及计算区间和的问题时非常有用!
如计算 下标2-5的数组元素和 如图示

C++代码 面对大量数据 读取 输出操作,最好用scanf 和 printf,耗时会小很多
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n, a, b;
cin >> n;
vector<int> vec(n);
vector<int> p(n);
int presum = 0;
for (int i = 0; i < n; i++) {
scanf("%d", &vec[i]);
presum += vec[i];
p[i] = presum;
}
while (~scanf("%d%d", &a, &b)) {
int sum;
if (a == 0) sum = p[b];
else sum = p[b] - p[a - 1];
printf("%d\n", sum);
}
}
JS(Node)版本代码
正好通过这个学习一下Node 还有ACM/面试模式!
之前还不知道JS怎么实现键盘录入 (扶额苦笑 呵呵呵哈哈哈)
注释拉满!
// 引入Node.js内置的readline模块,用于逐行读取输入
const readline = require('readline');
// 创建readline接口实例,配置输入输出流
const rl = readline.createInterface({
input: process.stdin, // 标准输入(键盘输入)
output: process.stdout // 标准输出(控制台输出)
});
let n = 0; //数组长度
let array = []; //被查询的数组
let queries = []; //查询的数组 记录查询左右边界
let lineCount = 0; //用lineCount判断输入内容
// 监听'line'事件:每当用户输入一行并按回车时触发
rl.on('line', (line) => {
if (lineCount === 0) {
//第一次输入 是n的值
n = parseInt(line);
lineCount++;
} else if (lineCount <= n) {
//后面的n个数 是数组元素值
array.push(parseInt(line));
lineCount++;
} else {
//最后的输入是查询边界
const [a, b] = line.trim().split(' ').map(Number);
queries.push([a, b]);
}
});
//监听'close'事件:当输入结束时触发(通常是按Ctrl+C或输入流关闭)
rl.on('close', () => {
// 构建前缀和数组
const prefix = new Array(n + 1).fill(0);
for (let i = 0; i < n; i++) {
prefix[i + 1] = prefix[i] + array[i];
}
// 处理每个查询
for (const [a, b] of queries) {
//注意边界的调整
const sum = prefix[b + 1] - prefix[a];
console.log(sum);
}
});二维前缀和 开发商购买土地
基本思想类似于普通的前缀和 不过这里是二维情况
JS代码如下
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let n, m;
let s = [];
let data = [];
let lineCount = 0;
rl.on('line', (line) => {
if (lineCount === 0) {
[n, m] = line.trim().split(' ').map(Number);
s = Array.from({ length: n + 1 }, () => new Array(m + 1).fill(0));
lineCount++;
} else {
data.push(line.trim().split(' ').map(Number));
if (data.length === n) {
// 构建二维前缀和数组
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= m; j++) {
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + data[i - 1][j - 1];
}
}
let ans = 1e9;
// 水平切割
for (let i = 1; i < n; i++) {
let x = Math.abs(s[n][m] - 2 * s[i][m]);
ans = Math.min(ans, x);
}
// 垂直切割
for (let i = 1; i < m; i++) {
let x = Math.abs(s[n][m] - 2 * s[n][i]);
ans = Math.min(ans, x);
}
console.log(ans);
rl.close();
}
}
});关键代码如下 是构建二维前缀和数组的关键!
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + data[i - 1][j - 1];总结
数组模块主要学习了以下几个方法
1.二分查找
2.双指针
3.滑动窗口
4.前缀和
也通过后面两个题目学习到Node环境下写算法的一些处理方式
链表
这一块主要要学习的不仅是问题的解决 还有如何用JS来实现数据结构 (之前都是用C/C++实现的)
移除链表元素 小试牛刀
很简单 就是用JS写链表题有点陌生……
var removeElements = function(head, val) {
let ret = new ListNode(0, head);
let curr = ret;
while (curr.next) {
if (curr.next.val === val) {
curr.next = curr.next.next;
// 这里不移动curr,以便检查新的curr.next
} else {
curr = curr.next; // 只有当下一个节点不需要删除时才移动
}
}
return ret.next;
};设计链表 JS的类
constructor
constructor 是 JavaScript 类中的特殊方法,用于创建和初始化类的实例对象
当使用 new 关键字创建实例时自动调用
如果不写会怎么样?
class ListNode {
// 没有写 constructor
}
// JavaScript 会自动添加:
// constructor() {}
const node = new ListNode();
console.log(node); // ListNode {} (空对象)构造函数写法
原来的写法
let MyLinkedList = function() {
this.size = 0;
this.head = new ListNode(0);
};等价的ES6 Class写法
class MyLinkedList {
constructor() {
this.size = 0;
this.head = new ListNode(0);
}
}static
static 关键字用于定义静态方法 通过类直接调用 this指向类本身 不能访问实例成员
// 通过类名直接调用
const list = MyLinkedList.fromArray([1, 2, 3]);static fromArray(arr) {
// 这里的 this 指向 MyLinkedList 类本身
const list = new this(); // 相当于 new MyLinkedList()
// ...
}
class MyLinkedList {
constructor() {
this.size = 0; // 实例属性
}
static fromArray(arr) {
console.log(this.size); // undefined,无法访问实例属性
// 只能访问静态属性和方法
}
}实际使用示例
// 创建链表的几种方式:
// 1. 传统方式
const list1 = new MyLinkedList();
list1.addAtTail(1);
list1.addAtTail(2);
list1.addAtTail(3);
// 2. 使用静态工厂方法
const list2 = MyLinkedList.fromArray([1, 2, 3]);
// 两种方式结果相同,但第二种更简洁最终实现代码 用ES6+实现 毕竟时代在进步嘛
// 链表节点类
class ListNode {
constructor(val = 0, next = null) {
this.val = val;
this.next = next;
}
}
// 链表类
class MyLinkedList {
constructor() {
this.size = 0;
this.head = new ListNode(0); // 虚拟头节点
}
// 获取指定位置的节点值
get(index) {
if (index < 0 || index >= this.size) {
return -1;
}
let current = this.head;
for (let i = 0; i <= index; i++) {
current = current.next;
}
return current.val;
}
// 在头部添加节点
addAtHead(val) {
this.addAtIndex(0, val);
}
// 在尾部添加节点
addAtTail(val) {
this.addAtIndex(this.size, val);
}
// 在指定位置添加节点
addAtIndex(index, val) {
if (index > this.size) return;
index = Math.max(0, index); // 处理负索引
let prev = this.head;
for (let i = 0; i < index; i++) {
prev = prev.next;
}
const newNode = new ListNode(val, prev.next);
prev.next = newNode;
this.size++;
}
// 删除指定位置的节点
deleteAtIndex(index) {
if (index < 0 || index >= this.size) return;
let prev = this.head;
for (let i = 0; i < index; i++) {
prev = prev.next;
}
prev.next = prev.next.next;
this.size--;
}
// 可选:转换为数组(便于调试和测试)
toArray() {
const result = [];
let current = this.head.next;
while (current !== null) {
result.push(current.val);
current = current.next;
}
return result;
}
// 可选:从数组创建链表(静态工厂方法)
static fromArray(arr) {
const list = new MyLinkedList();
arr.forEach(val => list.addAtTail(val));
return list;
}
// 可选:打印链表(调试用)
print() {
console.log(this.toArray().join(' -> '));
}
}
// 使用示例
const list = new MyLinkedList();
list.addAtHead(1);
list.addAtTail(3);
list.addAtIndex(1, 2); // 链表: 1 -> 2 -> 3
console.log(list.get(1)); // 2
list.deleteAtIndex(1); // 链表: 1 -> 3
console.log(list.get(1)); // 3
// 使用静态工厂方法
const list2 = MyLinkedList.fromArray([4, 5, 6]);
list2.print(); // 4 -> 5 -> 6反转链表 双指针 or 递归
双指针
示意图:
https://pic.leetcode-cn.com/1631933586-mEtOBg-008eGmZEly1gnrf1oboupg30gy0c44qp.gif
// 双指针:
var reverseList = function(head) {
if(!head || !head.next) return head;
let temp = null, pre = null, cur = head;
while(cur) {
temp = cur.next;
cur.next = pre;
pre = cur;
cur = temp;
}
// temp = cur = null;
return pre;
};
递归解决
// 递归:
var reverse = function(pre, head) {
if(!head) return pre;
const temp = head.next;
head.next = pre;
pre = head
return reverse(pre, temp);
}
var reverseList = function(head) {
return reverse(null, head);
};
两两交换链表中的节点
把逻辑搞清楚即可!
(dummy : 虚拟节点)
var swapPairs = function (head) {
const dummy = new ListNode(0, head);
let current = dummy;
while (current.next && current.next.next) {
//循环条件不能交换位置
//因为必须先检查temp.next存在,才能安全地访问temp.next.next
const first = current.next;
const second = current.next.next;
// 交换节点
first.next = second.next;
second.next = first;
current.next = second;
// 移动到下一对的前一个节点
current = first;
}
return dummy.next;
};递归版本
var swapPairs = function (head) {
if (head == null || head.next == null) {
return head;
}
let after = head.next;
head.next = swapPairs(after.next);
after.next = head;
return after;
};
删除链表的倒数第N个结点 快慢指针
首先这里我推荐大家使用虚拟头结点,这样方便处理删除实际头结点的逻辑,如果虚拟头结点不清楚,可以看这篇: 链表:听说用虚拟头节点会方便很多?
删除一个结点 需要找到这个结点的前一个结点!
若没有虚拟头结点 则删除头结点操作需要单独处理!
var removeNthFromEnd = function (head, n) {
// 创建哨兵节点,简化解题逻辑
let dummy = new ListNode(0,head)
let fast = dummy
let slow = dummy
while(n--){
fast = fast.next
}
while(fast.next){
fast = fast.next
slow = slow.next
}
slow.next = slow.next.next
return dummy.next
}链表相交 先走一步 解构赋值交换数据
看如下两个链表,目前curA指向链表A的头结点,curB指向链表B的头结点:

我们求出两个链表的长度,并求出两个链表长度的差值,然后让curA移动到,和curB 末尾对齐的位置,如图:
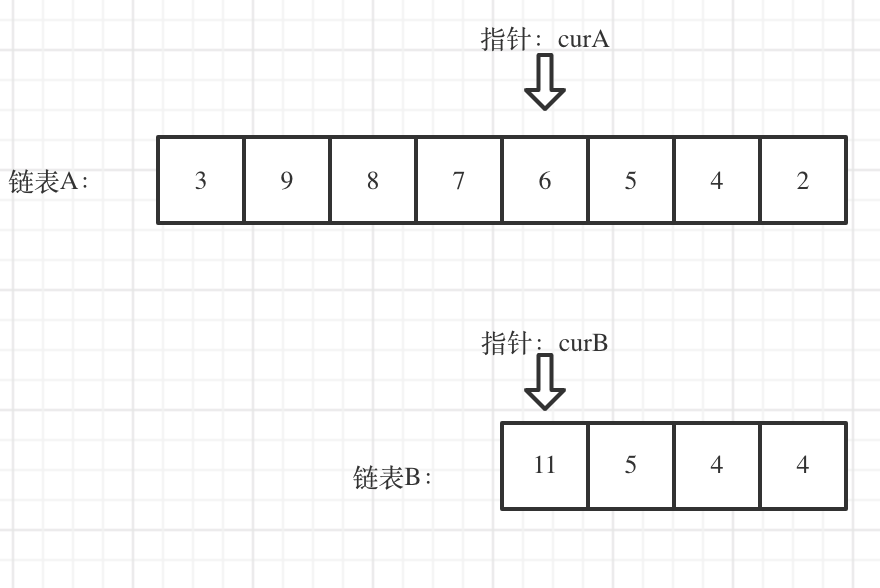
此时我们就可以比较curA和curB是否相同,如果不相同,同时向后移动curA和curB,如果遇到curA == curB,则找到交点
否则循环退出返回空指针
var getListLen = function(head) {
let len = 0, cur = head;
while(cur) {
len++;
cur = cur.next;
}
return len;
}
var getIntersectionNode = function(headA, headB) {
let curA = headA,curB = headB,
lenA = getListLen(headA), // 求链表A的长度
lenB = getListLen(headB);
if(lenA < lenB) { // 让curA为最长链表的头,lenA为其长度
// 交换变量注意加 “分号” ,两个数组交换变量在同一个作用域下时
// 如果不加分号,下面两条代码等同于一条代码: [curA, curB] = [lenB, lenA]
[curA, curB] = [curB, curA];
[lenA, lenB] = [lenB, lenA];
}
let i = lenA - lenB; // 求长度差
while(i-- > 0) { // 让curA和curB在同一起点上(末尾位置对齐)
curA = curA.next;
}
while(curA && curA !== curB) { // 遍历curA 和 curB,遇到相同则直接返回
curA = curA.next;
curB = curB.next;
}
return curA;
};注意这里的操作!
[curA, curB] = [curB, curA];
[lenA, lenB] = [lenB, lenA];这里是利用解构赋值进行数据交换 固定curA为最长链表的头,lenA为其长度
传统方法使用temp作为中间变量 很不美观
这种写法使用了 ES6 的解构赋值(Destructuring Assignment),它比传统的 temp 中间变量方法更加简洁和优雅
工作原理相当于创建了一个临时数组tempArray
// 相当于:
let tempArray = [bLen, aLen];
aLen = tempArray[0]; // 第一个值赋给 aLen
bLen = tempArray[1]; // 第二个值赋给 bLen
// 但引擎会优化这个过程,不会真的创建临时数组
// 必须要加分号! 否则相当于[curA, curB] = [curB, curA][lenA, lenB] = [lenB, lenA]
// 这不是我们想要的效果!
解构赋值的其他应用
// 交换多个变量
[a, b, c] = [c, a, b];
// 函数返回多个值
function getValues() { return [1, 2, 3]; }
const [x, y, z] = getValues();
// 对象解构
const {name, age} = person;环形链表 哈希表 or 依旧快慢指针
哈希表
我们遍历链表中的每个节点,并将它记录下来;一旦遇到了此前遍历过的节点,就可以判定链表中存在环 借助哈希表可以很方便地实现
此操作可以利用JS中的内置对象Set轻松实现
var detectCycle = function(head) {
const visted = new Set()
while(head!==null){
if(visted.has(head)){
return head
}
visted.add(head)
head = head.next
}
return null
}快慢指针
1.判断链表是否有环
可以使用快慢指针法,分别定义 fast 和 slow 指针,从头结点出发,fast指针每次移动两个节点,slow指针每次移动一个节点,如果 fast 和 slow指针在途中相遇 ,说明这个链表有环
为什么fast 走两个节点,slow走一个节点,有环的话,一定会在环内相遇呢,而不是永远的错开呢?
首先第一点:fast指针一定先进入环中,如果fast指针和slow指针相遇的话,一定是在环中相遇,这是毋庸置疑的
那么来看一下,为什么fast指针和slow指针一定会相遇呢?
这是因为fast是走两步,slow是走一步,其实相对于slow来说,fast是一个节点一个节点的靠近slow的,所以fast一定可以和slow重合
2.如果有环 如何找到这个环的入口?
如下图所示,设链表中环外部分的长度为 a。slow 指针进入环后,又走了 b 的距离与 fast 相遇。此时,fast 指针已经走完了环的 n 圈,因此它走过的总距离为 a+n(b+c)+b=a+(n+1)b+nc

根据题意,任意时刻,fast 指针走过的距离都为 slow 指针的 2 倍
因此,我们有a+(n+1)b+nc=2(a+b)⟹a=c+(n−1)(b+c)
有了 a=c+(n−1)(b+c) 的等量关系,我们会发现:从相遇点到入环点的距离加上 n−1 圈的环长,恰好等于从链表头部到入环点的距离
var detectCycle = (head)=> {
//如果没有节点或者只有一个节点 则肯定无环
if(!head || !head.next) return null;
//如果快慢指针不会相遇 也无环
let slow =head.next, fast = head.next.next;
while(fast && fast.next && fast!== slow) {
slow = slow.next;
fast = fast.next.next;
}
if(!fast || !fast.next ) return null;
//已经确定有环 根据我们之前的分析去找到环的入口即可
slow = head;
while (fast !== slow) {
slow = slow.next;
fast = fast.next;
}
return slow;
};
哈希表
有效的字母异位词 对象hashMap or 数组hashMap
数组
charCodeAt() 是 JavaScript 字符串的方法,用于获取指定位置字符的 Unicode 编码值
为什么要用base?
如果没有 base,你的数组索引会是:
“a” -> 97, “b” -> 98, …, “z” -> 122
这意味着你需要一个长度为123的数组,而不是26!
var isAnagram = function(s, t) {
if(s.length !== t.length) return false
const base = "a".charCodeAt()
const ret = new Array(26).fill(0)
for(const char of s) {
ret[char.charCodeAt() - base]++
}
for(const char of t){
if(!ret[char.charCodeAt() -base])return false
ret[char.charCodeAt() -base]--
}
return true
};对象
const initHashMap = (len,str) =>{
const hashMap = {}
for(let i = 0;i<len ;i++){
hashMap[str[i]] = (hashMap[str[i]] || 0) + 1
}
return hashMap
}
var isAnagram = function(s, t) {
if (s.length !== t.length) return false
let len = s.length
const mapS = initHashMap(len,s)
const mapT = initHashMap(len,t)
for(const char in mapS){
if(mapS[char] !== mapT[char]){
return false
}
}
return true
}
for…of 不能直接遍历普通对象
mapS 是一个对象,而 for…of 只能用于可迭代对象(如数组、字符串、Map、Set等),不能直接用于普通对象
要用for…in 遍历普通对象的键
两个数组的交集 Set操作
老实人
function intersection(nums1: number[], nums2: number[]): number[] {
let resSet : Set<number> = new Set()
let nums1Set : Set<number> = new Set(nums1)
// for(const n of nums2) {
// nums1Set.has(n) && resSet.add(n);
// }
// 循环 比 迭代器快
for (let i = nums2.length - 1; i >= 0; i--) {
nums1Set.has(nums2[i]) && resSet.add(nums2[i]);
}
//return [...resSet] //将集合转换为数组
return Array.from(resSet) //将集合转换为数组
};小炫技
const intersection = (nums1: number[], nums2: number[]):number[]=> {
return Array.from(new Set(nums1.filter(i => nums2.includes(i))))
};快乐数 无限循环 必会重现

解决问题的关键就在于 无限循环 这意味着 如果一个数不是快乐数 一个过程的结果值必会重复!
可以根据这个性质来进行判断 将每次算出来的结果放在一个Set()中 如果重复出现 则说明 这个数不是快乐数!
方法一 代数求和
function calcSum(val: number): number {
//计算一个数的每个位置上数字的平方和
let sum = 0
while(val) {
let num = val % 10
sum+= num**2
val = Math.floor((val/10))
}
return sum
}
function isHappy(n: number): boolean {
let storeSet: Set<number> = new Set()
while (n !== 1 && !storeSet.has(n)) {
storeSet.add(n);
n = calcSum(n);
}
return n === 1;
};方法二 转为字符串使用reduce求和
function calcSum(val: number): number {
//计算一个数的每个位置上数字的平方和
return String(val).split("").reduce((pre, cur) => (pre + Number(cur) * Number(cur)), 0)
}
function isHappy(n: number): boolean {
let storeSet: Set<number> = new Set()
while (n !== 1 && !storeSet.has(n)) {
storeSet.add(n);
n = calcSum(n);
}
return n === 1;
};美妙!
两数之和 经典老题 Map发力
再强调一下 什么时候使用哈希法,当我们需要查询一个元素是否出现过,或者一个元素是否在集合里的时候,就要第一时间想到哈希法
本题,我们不仅要知道元素有没有遍历过,还要知道这个元素对应的下标,需要使用 key value结构来存放,key来存元素,value来存下标,那么使用map正合适
Map操作以及Map和对象的区别
Map的基本操作
const map = new Map();
// 添加/设置元素
map.set('name', 'John');
map.set(1, 'number one');
map.set({id: 1}, 'object key');
// 获取元素
map.get('name'); // 'John'
map.get('nonexistent'); // undefined
// 检查是否存在
map.has('name'); // true
// 删除元素
map.delete('name');
// 清空 Map
map.clear();
// 获取元素数量
map.size; // 0Map的遍历操作
const map = new Map([['a', 1], ['b', 2], ['c', 3]]); //使用二维数组创建Map
// for...of 遍历
for (let [key, value] of map) {
console.log(key, value);
}
// 只遍历键
for (let key of map.keys()) {
console.log(key);
}
// 只遍历值
for (let value of map.values()) {
console.log(value);
}
// 遍历键值对
for (let [key, value] of map.entries()) {
console.log(key, value);
}Map的转换方法
const map = new Map([['a', 1], ['b', 2]]);
// 转为数组
Array.from(map); // [['a', 1], ['b', 2]]
Array.from(map.keys()); // ['a', 'b']
Array.from(map.values()); // [1, 2]
// 转为对象
Object.fromEntries(map); // {a: 1, b: 2}Map与Object
- 键的类型:Map 的键可以是任何类型,Object 的键只能是字符串或 Symbol
- 顺序保证:Map 保持插入顺序
- 大小获取:Map 有 size 属性,Object 需要手动计算
- 性能:频繁增删操作时 Map 性能更好
过程模拟


function twoSum(nums: number[], target: number): number[] {
//建立一个从数值映射到索引的Map
const valueToIndex: Map<number,number> = new Map()
for(let i = 0;i<nums.length;i++){
let element = target - nums[i] //看看需要什么数字
if(valueToIndex.get(element) !== undefined){ //如果需要的数字存在
return [valueToIndex.get(element),i] //返回两个数的索引
}
valueToIndex.set(nums[i],i) //若需要的数不存在 就将当前数字和索引存入Map
}
return [] //一直没找到那就返回一个空数组
}四数相加 II 空间换时间 两两分组
const fourSumCount = (A, B, C, D) => {
const countAB = new Map() //创建一个Map 存放(前两个数组和 : 出现次数)
A.forEach(u => B.forEach(v => countAB.set(u + v, (countAB.get(u + v) || 0) + 1)))//构建Map
let ans = 0
for (let u of C) {
for (let v of D) {
if (countAB.has(-u - v)) {
ans += countAB.get(-u - v)
}
}
}
return ans
}
赎金信 Map or 数组哈希

Map
使用一个map记录ransomNote中出现的字母个数 然后遍历magazine进行操作
出现一次一样的字母就在map中减少对应的字母出现字数
如果出现次数为0 就在map中删除这个字母
最后如果map的size为0就说明满足条件
var canConstruct = function(ransomNote, magazine) {
if(ransomNote.length > magazine.length)return false
const countMap = new Map() //建立map 记录ransomNote中各字母出现次数
//填充map
for(const char of ransomNote){
countMap.set(char,(countMap.get(char) || 0) + 1)
}
//magazine与map进行比对
for(const char of magazine){
if(countMap.has(char)){
//设置remaining变量减少不必要的操作
const remaining = countMap.get(char) - 1
if( remaining === 0 ) {
countMap.delete(char)
}
else {
countMap.set(char,remaining)
}
if(countMap.size === 0)return true //已经满足!提前返回
}
}
return countMap.size === 0
}数组模拟
思路差不多 不仔细说了
var canConstruct = function(ransomNote, magazine) {
const map = new Array(26).fill(0)
const base = "a".charCodeAt()
for(let i = 0 ;i<magazine.length;i++){
map[magazine[i].charCodeAt() - base]++
}
for(let i = 0 ;i<ransomNote.length;i++){
const index = ransomNote[i].charCodeAt() - base
if(!map[index])return false
map[index]--
}
return true
}三数之和 哈希表不便 -> 双指针!
哈希表去重很麻烦 这里改用双指针!
算法复杂度O(n^2)
实现思路如下图
https://file1.kamacoder.com/i/algo/15.%E4%B8%89%E6%95%B0%E4%B9%8B%E5%92%8C.gif
双指针 –> 先排序!
这里需要进行去重操作
function threeSum(nums: number[]): number[][] {
nums.sort((a, b) => a - b); //排序
let length = nums.length;
let left: number = 0,
right: number = length - 1;
let resArr: number[][] = [];
for (let i = 0; i < length; i++) {
if (nums[i]>0) {
return resArr; //nums经过排序后,只要nums[i]>0, 此后的nums[i] + nums[left] + nums[right]均大于0,可以提前终止循环。
}
if (i > 0 && nums[i] === nums[i - 1]) {
continue;
} //和前一个相等就不必再考虑了
left = i + 1;
right = length - 1;
while (left < right) {
let total: number = nums[i] + nums[left] + nums[right];
if (total === 0) {
resArr.push([nums[i], nums[left], nums[right]]);
left++;
right--;
while (nums[right] === nums[right + 1]) {
right--; //相等就不用再考虑了
}
while (nums[left] === nums[left - 1]) {
left++; //相等就不用再考虑了
}
} else if (total < 0) {
left++;
} else {
right--;
}
}
}
return resArr;
}疑问: 为什么两数之和不用双指针??
因为此题需要返回满足情况的数的数组 可以进行排序操作
而两数之和的题要求返回下标 使用双指针进行排序后下标就混乱了
四数之和 思路一致 依旧双指
var fourSum = function(nums, target) {
const len = nums.length;
if(len < 4) return [];
nums.sort((a, b) => a - b);
const res = [];
for(let i = 0; i < len - 3; i++) {
// 去重i
if(i > 0 && nums[i] === nums[i - 1]) continue;
for(let j = i + 1; j < len - 2; j++) {
// 去重j
if(j > i + 1 && nums[j] === nums[j - 1]) continue;
let l = j + 1, r = len - 1;
while(l < r) {
const sum = nums[i] + nums[j] + nums[l] + nums[r];
if(sum < target) { l++; continue}
if(sum > target) { r--; continue}
res.push([nums[i], nums[j], nums[l], nums[r]]);
// 对nums[left]和nums[right]去重
while(l < r && nums[l] === nums[++l]);
while(l < r && nums[r] === nums[--r]);
}
}
}
return res;
};字符串
反转字符串 直接调库 or 双指针
极简代码
const reverseString = s => s.reverse()注意: 字符串本身是没有reverse方法的 但是数组是有的 不要搞混了
双指针
原理很简单 并不多说了
function reverseString(s: string[]): void {
let l:number = 0
let r:number = s.length - 1
while(l<r){
[s[l],s[r]] = [s[r],s[l]]
l++
r--
}
}反转字符串II 分块治之
我的想法是把字符串每k个分为一组 每组分开处理
然后根据题目特性 如果这一组是第奇数组 那么就要进行翻转
最后再把所有的字符串拼到一起就可以了
这里用到了字符串的slice()方法 –> 截取子串
var reverseStr = function(s, k) {
const result = [];
for (let i = 0; i < s.length; i += k) {
let block = s.slice(i, i + k);
// slice(start, end) -> 提取子字符串
// "hello".slice(1, 3) → "el"
// 每隔一块反转一次(奇数索引块反转)
if (Math.floor(i / k) % 2 === 0) {
block = block.split('').reverse().join('');
}
result.push(block);
}
return result.join('');
}另一方法
var reverseStr = function(s, k) {
const len = s.length;
let resArr = s.split("");
for(let i = 0; i < len; i += 2 * k) { // 每隔 2k 个字符的前 k 个字符进行反转
let l = i - 1, r = i + k > len ? len : i + k;
while(++l < --r) [resArr[l], resArr[r]] = [resArr[r], resArr[l]];
}
return resArr.join("");
};替换数字 直接判断 or 扩容赋值
直接判断
const readline = require('readline');
const rl = readline.createInterface({ input: process.stdin, output: process.stdout });
rl.on('line', line => console.log(line.replace(/\d/g, 'number')));扩容赋值

首先扩充数组到每个数字字符替换成 “number” 之后的大小
例如 字符串 “a5b” 的长度为3,那么 将 数字字符变成字符串 “number” 之后的字符串为 “anumberb” 长度为 8
为什么要从后向前填充,从前向后填充不行么?
从前向后填充就是O(n^2)的算法了,因为每次添加元素都要将添加元素之后的所有元素整体向后移动
其实很多数组填充类的问题,其做法都是先预先给数组扩容带填充后的大小,然后在从后向前进行操作
这么做有两个好处:
- 不用申请新数组。
- 从后向前填充元素,避免了从前向后填充元素时,每次添加元素都要将添加元素之后的所有元素向后移动的问题
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
})
function main() {
const num0 = "0".charCodeAt();
const num9 = "9".charCodeAt();
const a = "a".charCodeAt();
const z = "z".charCodeAt();
function isAZ(str) {
return str >= a && str <= z;
}
function isNumber(str) {
return str >= num0 && str <= num9;
}
rl.on("line", (input) => {
let n = 0;
for (let i = 0; i < input.length; i++) {
const val = input[i].charCodeAt();
if (isNumber(val)) {
n += 6;
}
if (isAZ(val)) {
n++;
}
}
const ans = new Array(n).fill(0);
let index = input.length - 1;
for (let i = n - 1; i >= 0; i--) {
const val = input[index].charCodeAt();
if (isAZ(val)) {
ans[i] = input[index];
}
if (isNumber(val)) {
ans[i] = "r";
ans[i - 1] = "e";
ans[i - 2] = "b";
ans[i - 3] = "m";
ans[i - 4] = "u";
ans[i - 5] = "n";
i -= 5;
}
index--;
}
console.log(ans.join(""));
})
}
main();反转字符串中的单词 移除空格
我的方法 简单易懂
var reverseWords = function(s) {
const str = s.trim().split(' ').reverse()
const strArray = str.filter(item => item.length !==0)
return strArray.join(' ')
}更简单的写法 LeetCode官方题解
var reverseWords = function(s) {
return s.trim().split(/\s+/).reverse().join(' ')
// /\s+/ 的意思是:匹配一个或多个空白字符 正则表达式
};
右旋字符串 反转再反转!
我的做法 申请了额外空间 时间复杂度O(n)
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let lineCount = 0;
let k;
let str;
rl.on('line', (line) => {
if (lineCount === 0) {
k = Number(line.trim());
lineCount++;
} else {
str = line.trim();
rl.close(); // 读取到第二行后关闭
}
})
rl.on('close', () => {
const len = str.length
let after = ''
let before = ''
let res = ''
for (let i = 0; i < len - k; i++) {
after += str[i]
}
for (let i = len - k; i < len; i++) {
before += str[i]
}
res+=before
res+=after
console.log(res)
})如果要求不申请额外空间 就要想到别的办法
可以先给整体字符串反转
再给两段分别反转 这样就可以实现O(1)空间复杂度解决问题
过程为:
abcdefg —> gfedcba –> fgabcde
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let lineCount = 0;
let k;
let str;
rl.on('line', (line) => {
if (lineCount === 0) {
k = Number(line.trim());
lineCount++;
} else {
str = line.trim();
rl.close();
}
});
rl.on('close', () => {
// 将字符串转换为数组以便原地操作
const arr = str.split('');
const len = arr.length;
// 处理k大于字符串长度的情况
k = k % len;
if (k === 0) {
console.log(str);
return;
}
// 三次反转法
// 1. 反转整个字符串
reverse(arr, 0, len - 1);
// 2. 反转前k个字符
reverse(arr, 0, k - 1);
// 3. 反转剩余字符
reverse(arr, k, len - 1);
console.log(arr.join(''));
});
// 原地反转数组的辅助函数
function reverse(arr, start, end) {
while (start < end) {
const temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
start++;
end--;
}
}注意!!! 要对数组进行反转操作 而不是对字符串进行反转!!!
原因如下:
- 字符串不可变性:JavaScript中的字符串是不可变的(immutable),你不能像数组那样直接通过索引修改字符串中的字符。
str[start] = str[end]这样的操作不会实际改变字符串。 - 参数类型不匹配:
reverse函数期望第一个参数是数组(可修改),但你传入的是字符串(不可修改)。 - 解构赋值问题:即使传入数组,
[str[end], str[start]] = [str[start], str[end]]这种写法在字符串上也不起作用。
KMP算法 …… 暂时搁置
栈与队列
用栈实现队列
需要两个栈一个输入栈,一个输出栈
在push数据的时候,只要数据放进输入栈就好,但在pop的时候,操作就复杂一些,输出栈如果为空,就把进栈数据全部导入进来(注意是全部导入),再从出栈弹出数据,如果输出栈不为空,则直接从出栈弹出数据就可以了
最后如何判断队列为空呢?如果进栈和出栈都为空的话,说明模拟的队列为空了
var MyQueue = function() {
this.stackIn = [];
this.stackOut = [];
};
MyQueue.prototype.push = function(x) {
this.stackIn.push(x);
};
MyQueue.prototype.pop = function() {
const size = this.stackOut.length;
if(size) {
return this.stackOut.pop();
}
while(this.stackIn.length) {
this.stackOut.push(this.stackIn.pop());
}
return this.stackOut.pop();
};
MyQueue.prototype.peek = function() {
const x = this.pop();
this.stackOut.push(x);
return x;
};
MyQueue.prototype.empty = function() {
return !this.stackIn.length && !this.stackOut.length
};有效的括号 栈的经典题目
正常做法
const isValid = (s) => {
const stack = []
for (const char of s) {
if (char === '(' || char === '{' || char === '[') {
stack.push(char)
} else if (char === ')' || char === '}' || char === ']') {
// 还需要检查栈顶是否匹配
const top = stack[stack.length - 1]
if (
(char === ')' && top === '(') ||
(char === '}' && top === '{') ||
(char === ']' && top === '[')
) {
stack.pop()
}else {
return false
}
}
}
return stack.length === 0
}简化做法 —> 使用Map
const isValid = (s) => {
const stack = []
const map = {
'(': ')',
'[': ']',
'{': '}'
}
for (const char of s) {
if (char in map) { stack.push(char); continue }
if (map[stack.pop()] !== char) {
return false
}
}
return stack.length === 0
}动态规划
对于动态规划问题,可以拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
斐波那契数 经典入门
并不多说
const fib = (n) => {
const dp = new Array(n + 1).fill(0)
dp[0] = 0
dp[1] = 1
for (let i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2]
}
return dp[n]
}爬楼梯问题 依旧经典
并不多说
var climbStairs = function (n) {
// dp[i] : 爬到第i阶梯 可以的方法数
const dp = new Array(n + 1).fill(0)
dp[1] = 1
dp[2] = 2
for (let i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2]
}
return dp[n]
}使用最小花费爬楼梯 依旧经典
var minCostClimbingStairs = function(cost) {
const dp = [0, 0]
for (let i = 2; i <= cost.length; ++i) {
dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
}
return dp[cost.length]
}
不同路径 依旧经典

var uniquePaths = function(m, n) {
const dp = Array(m).fill().map(item => Array(n))
for (let i = 0; i < m; ++i) {
dp[i][0] = 1
}
for (let i = 0; i < n; ++i) {
dp[0][i] = 1
}
for (let i = 1; i < m; ++i) {
for (let j = 1; j < n; ++j) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
}
}
return dp[m - 1][n - 1]
};不同字符Ⅱ 路上有障碍 初始化控制
我原本还是按照上一题的方法去初始化 但是问题很多
所以可以在初始化的时候加上一个条件 只有不为障碍时才初始化为1
不满足初始化条件的循环直接终止即可 因为这条路已经行不通了!!! 直接舍弃
也就是说如果只看一条直线线路 上面有一个障碍 那后面的就会全为0
var uniquePathsWithObstacles = function (obstacleGrid) {
const m = obstacleGrid.length
const n = obstacleGrid[0].length
const dp = Array(m).fill().map(item => Array(n).fill(0))
for (let i = 0; i < m && obstacleGrid[i][0] === 0; ++i) {
dp[i][0] = 1
}
for (let i = 0; i < n && obstacleGrid[0][i] === 0; ++i) {
dp[0][i] = 1
}
for (let i = 1; i < m; ++i) {
for (let j = 1; j < n; ++j) {
dp[i][j] = obstacleGrid[i][j] === 1 ? 0 : dp[i - 1][j] + dp[i][j - 1]
}
}
return dp[m - 1][n - 1]
}
例子:
console.log(uniquePathsWithObstacles([[0, 1, 0, 0, 0], [1, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0]]))初始化后的dp数组长这样
[
[ 1, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0 ]
]
在红色处就已经被截断 后面的值全为0!!!
整数拆分 怎么拆?

1.确定dp数组含义
dp[i]:分拆数字i,可以得到的最大乘积为dp[i]
2.确定递推公式
可以从1遍历j,然后有两种渠道得到dp[i]
一个是j * (i – j) 直接相乘(拆成两个数相乘)
一个是j * dp[i – j],相当于是拆分(i – j) (拆成三个及以上的数相乘)
所以递推公式:dp[i] = max({dp[i], (i – j) * j, dp[i – j] * j})
3.dp数组初始化
dp[2] = 1,从dp[i]的定义来说,拆分数字2,得到的最大乘积是1
4.确定遍历顺序
先来看看递归公式:dp[i] = max(dp[i], max((i – j) * j, dp[i – j] * j));
dp[i] 是依靠 dp[i – j]的状态,所以遍历i一定是从前向后遍历,先有dp[i – j]再有dp[i]
for (int i = 3; i <= n ; i++) {
for (int j = 1; j <= i / 2; j++) {
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
}
}这里i/2是根据对称性所得 避免重复计算
也因为
对于乘积最大化的问题,拆分的数字尽可能接近时乘积最大(例如 3 * 3 = 9比 2 * 4 = 8大)
因此,j和 i - j越接近,乘积越大 j超过 i / 2后,i - j会小于 j,此时乘积不会比 j <= i / 2时更大
5.举例推导dp数组

分析完毕 代码如下
var integerBreak = function(n) {
let dp = new Array(n + 1).fill(0)
dp[2] = 1
for(let i = 3; i <= n; i++) {
for(let j = 1; j <= i / 2; j++) {
dp[i] = Math.max(dp[i], dp[i - j] * j, (i - j) * j)
}
}
return dp[n]
};打家劫舍 想好dp数组含义

1.确定dp数组以及下标的含义
dp[i]:考虑下标i(包括i)以内的房屋,最多可以偷窃的金额为dp[i]
2.确定递推公式
决定dp[i]的因素就是第i房间偷还是不偷
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1])3.dp数组初始化
dp[0] 一定是 nums[0],dp[1]就是nums[0]和nums[1]的最大值
4.确定遍历顺序
dp[i] 是根据dp[i – 2] 和 dp[i – 1] 推导出来的,那么一定是从前到后遍历
5.举例推导dp数组

JS代码
const rob = (nums) => {
const dp = new Array(nums.length).fill(0)
dp[0] = nums[0]
dp[1] = Math.max(nums[0], nums[1])
for (let i = 2; i < nums.length; i++) {
dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1])
}
return dp[nums.length - 1]
}打家劫舍Ⅱ 房屋围一圈再去偷
对于一个数组,成环的话主要有如下三种情况:
- 情况一:考虑不包含首尾元素
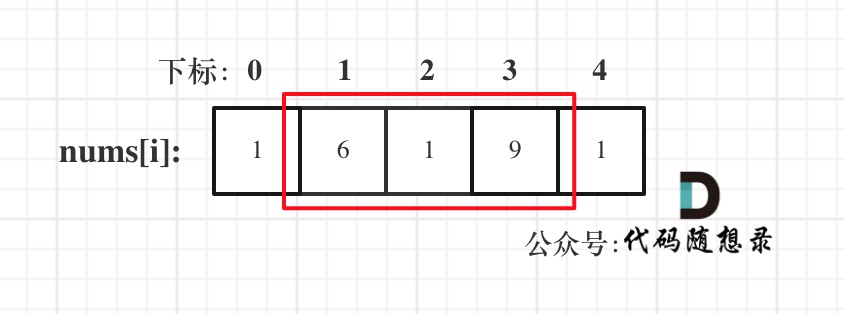
- 情况二:考虑包含首元素,不包含尾元素
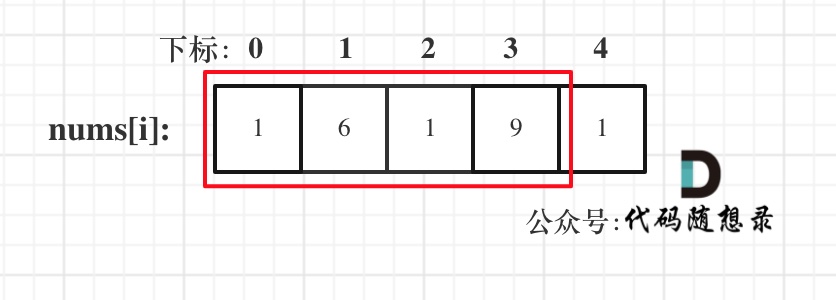
- 情况三:考虑包含尾元素,不包含首元素
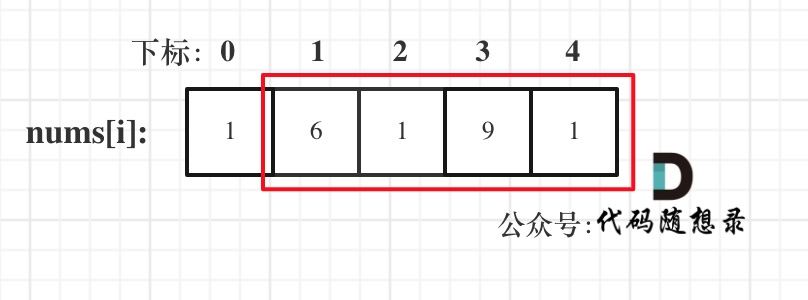
情况二 和 情况三 都包含了情况一了,所以只考虑情况二和情况三就可以了
情况一二三是“考虑”的范围,而具体房间偷与不偷交给递推公式去抉择
分析到这里 本题就简单了 剩下的和上一题一样
JS代码
var rob = function (nums) {
const n = nums.length
if (n === 0) return 0
if (n === 1) return nums[0]
const result1 = robRange(nums, 0, n - 2)
const result2 = robRange(nums, 1, n - 1)
return Math.max(result1, result2)
};
const robRange = (nums, start, end) => {
if (end === start) return nums[start]
const dp = Array(nums.length).fill(0)
dp[start] = nums[start]
dp[start + 1] = Math.max(nums[start], nums[start + 1])
for (let i = start + 2; i <= end; i++) {
dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1])
}
return dp[end]
}01背包—01二维dp
有n件物品和一个最多能背重量为w 的背包
第i件物品的重量是weight[i],得到的价值是value[i]
每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大

1.确定dp数组以及下标的含义
有三个维度 价值 重量 物品 => 可以构建一个二维表

这里每个格子都是一个dp[i][j]
dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少
2.确定递推公式
分成两种情况 选这件物品和不选这件物品
- 不选物品i:背包容量为j,里面不放物品i的最大价值是dp[i – 1][j]

- 选物品i:背包空出物品i的容量后,背包容量为j – weight[i],dp[i – 1][j – weight[i]] 为背包容量为j – weight[i]且不放物品i的最大价值,那么dp[i – 1][j – weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值

3.dp数组初始化
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品
4.确定遍历顺序
先遍历 物品还是先遍历背包重量呢 都可以
虽然两个for循环遍历的次序不同,但是dp[i][j]所需要的数据就是左上角,根本不影响dp[i][j]公式的推导
但先遍历物品再遍历背包容量这个顺序更好理解
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}5.举例推导dp数组

最终核心JS代码
for (let i = 1; i < n; i++) {
for (let j = 0; j <= bagweight; j++) {
if (j < weight[i]) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
}01背包—02滚动数组
观察到 每行运算 只和前面的一行有关系 跟再前面的没关系
可以先计算出第一行 根据第一行计算第二行 以此类推
这样一来只要表示下一行就可以了 可以减小空间复杂度
next[j] = Math.max(value[i] + result[j - weight[i]], result[j])最终JS代码

二叉树
二叉树理论基础
二叉树的遍历方式
二叉树主要有两种遍历方式:
- 深度优先遍历:先往深走,遇到叶子节点再往回走
- 广度优先遍历:一层一层的去遍历
这两种遍历是图论中最基本的两种遍历方式
那么从深度优先遍历和广度优先遍历进一步拓展,才有如下遍历方式:
- 深度优先遍历
- 前序遍历(递归法,迭代法)
- 中序遍历(递归法,迭代法)
- 后序遍历(递归法,迭代法)
- 广度优先遍历
- 层次遍历(迭代法)
在深度优先遍历中:有三个顺序,前中后序遍历
这里前中后,其实指的就是中间节点的遍历顺序
看如下中间节点的顺序,就可以发现,中间节点的顺序就是所谓的遍历方式
- 前序遍历:中左右
- 中序遍历:左中右
- 后序遍历:左右中
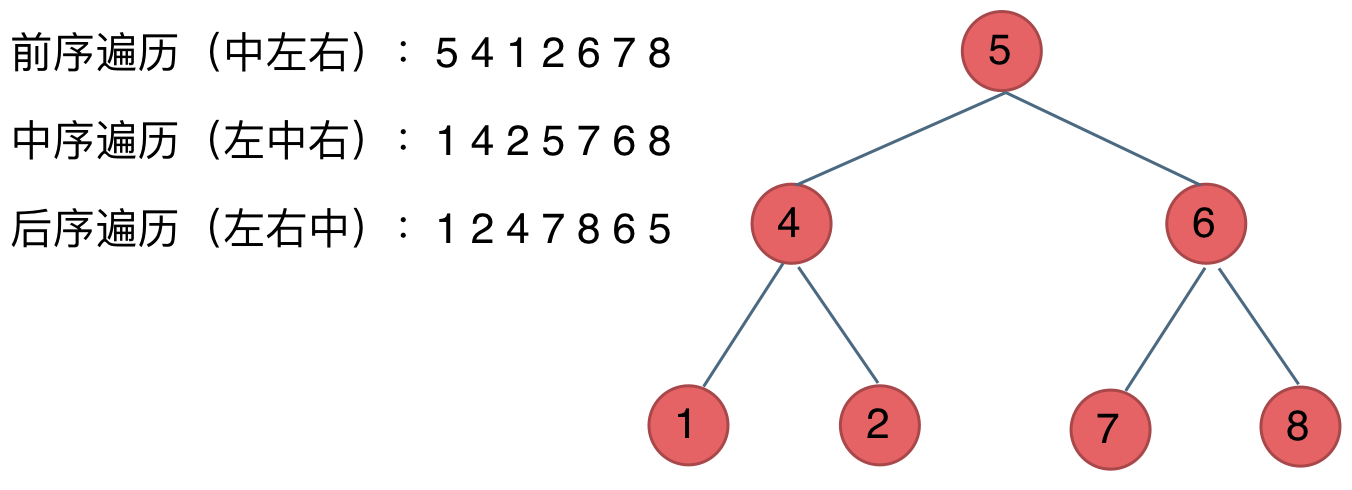
最后再说一说二叉树中深度优先和广度优先遍历实现方式,我们做二叉树相关题目,经常会使用递归的方式来实现深度优先遍历,也就是实现前中后序遍历,使用递归是比较方便的
之前我们讲栈与队列的时候,就说过栈其实就是递归的一种实现结构,也就说前中后序遍历的逻辑其实都是可以借助栈使用递归的方式来实现的
而广度优先遍历的实现一般使用队列来实现,这也是队列先进先出的特点所决定的,因为需要先进先出的结构,才能一层一层的来遍历二叉树
二叉树的定义
TS代码
class TreeNode {
public val: number
public left: TreeNode | null
public right: TreeNode | null
constructor(val?: number, left?: TreeNode, right?: TreeNode) {
this.val = val === undefined ? 0 : val
this.left = left === undefined ? null : left
this.right = right === undefined ? null : right
}
}二叉树的递归遍历 — 递归遍历与迭代遍历
每次写递归,都按照这三要素来写
- 确定递归函数的参数和返回值: 确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型
- 确定终止条件: 写完了递归算法, 运行的时候,经常会遇到栈溢出的错误,就是没写终止条件或者终止条件写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出
- 确定单层递归的逻辑: 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程
TS代码
// 前序遍历
// 确定参数和返回值
function preorderTraversal(node: TreeNode | null): number[] {
function traverse(node: TreeNode | null, res: number[]): void {
if (node === null) return; // 确定终止条件
// 单层递归逻辑
res.push(node.val);
traverse(node.left, res);
traverse(node.right, res);
}
const res: number[] = [];
traverse(node, res);
return res;
}
// 中序遍历
function inorderTraversal(node: TreeNode | null): number[] {
function traverse(node: TreeNode | null, res: number[]): void {
if (node === null) return;
traverse(node.left, res);
res.push(node.val);
traverse(node.right, res);
}
const res: number[] = [];
traverse(node, res);
return res;
}
// 后序遍历
function postorderTraversal(node: TreeNode | null): number[] {
function traverse(node: TreeNode | null, res: number[]): void {
if (node === null) return;
traverse(node.left, res);
traverse(node.right, res);
res.push(node.val);
}
const res: number[] = [];
traverse(node, res);
return res;
}二叉树的迭代遍历
代码示例

二叉树结构如下





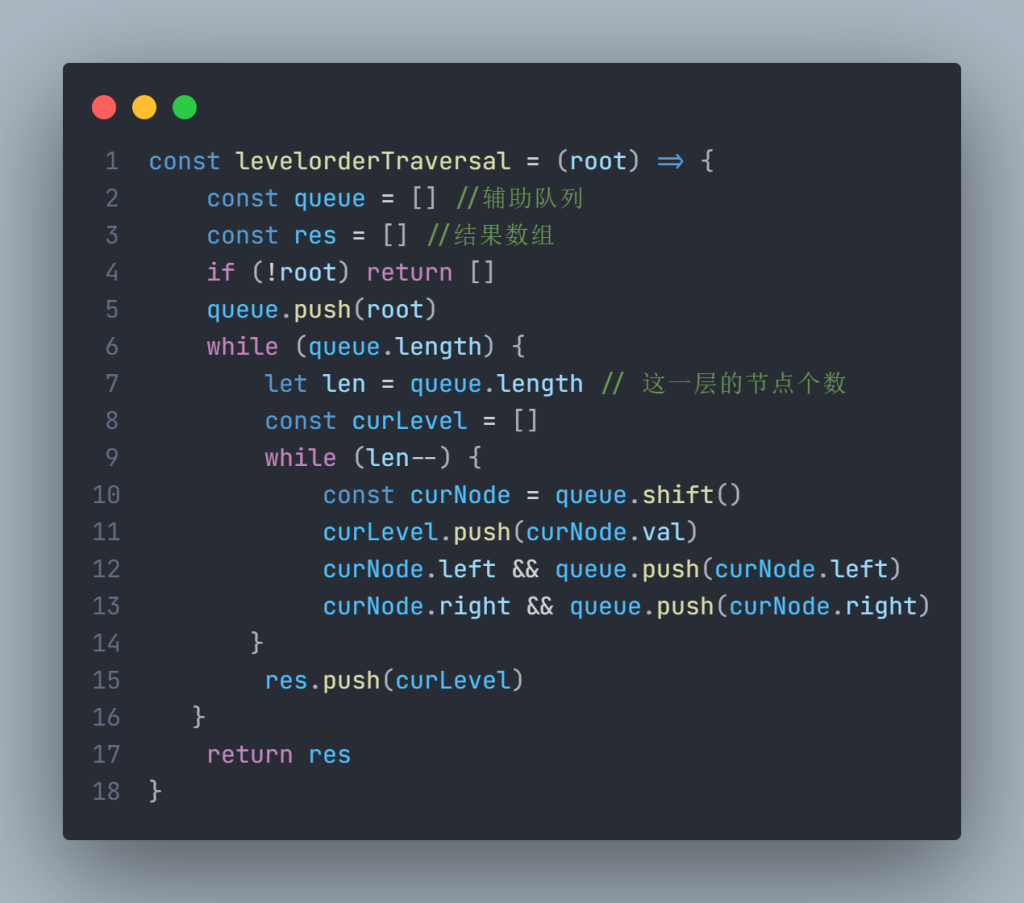
二叉树的层序遍历 — 辅助队列
图示
代码
回溯算法
组合问题
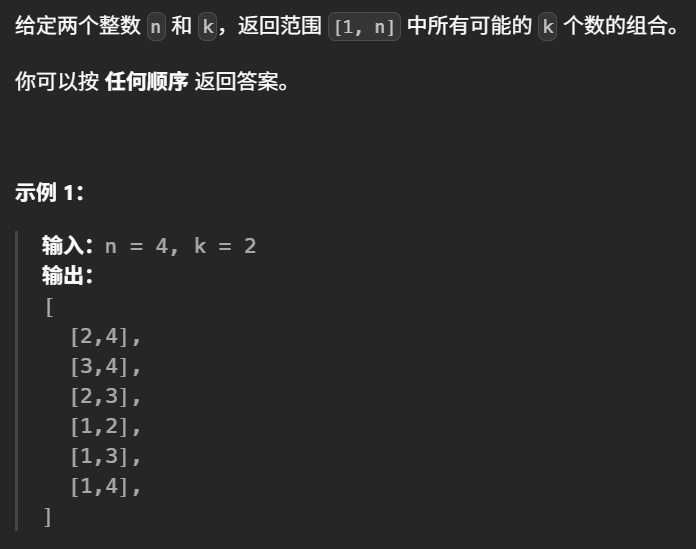
思路
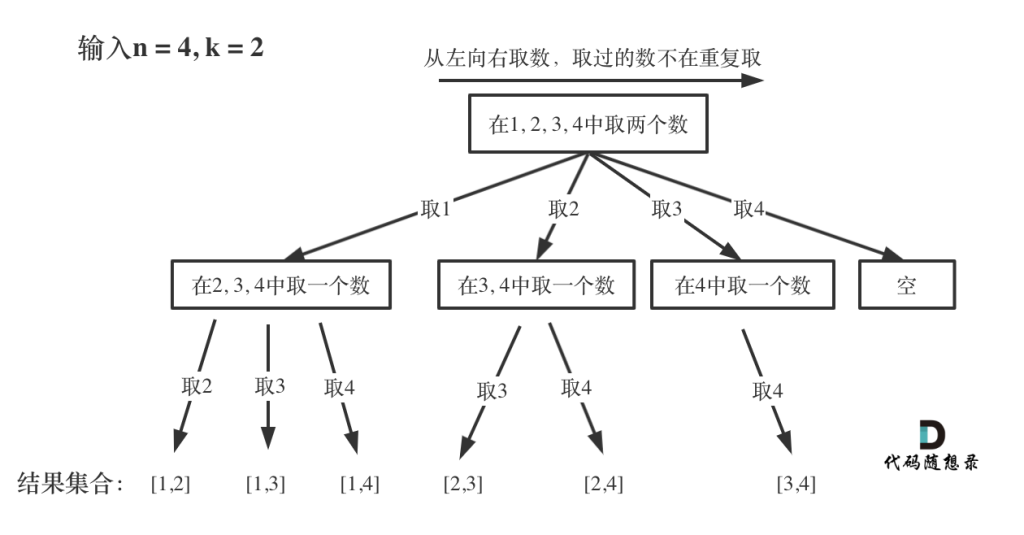
JS代码
var combine = function (n, k) {
// 回溯法
let result = []
let path = []
let backtracking = (n, k, startIndex) => {
// 终止条件
if (path.length === k) {
result.push(path.slice());
return;
}
// 循环本层集合元素
for (let i = startIndex; i <= n; i++) {
path.push(i);
// 递归
backtracking(n, k, i + 1);
// 回溯操作
path.pop();
}
};
backtracking(n, k, 1);
return result;
}
console.log(combine(4, 2))
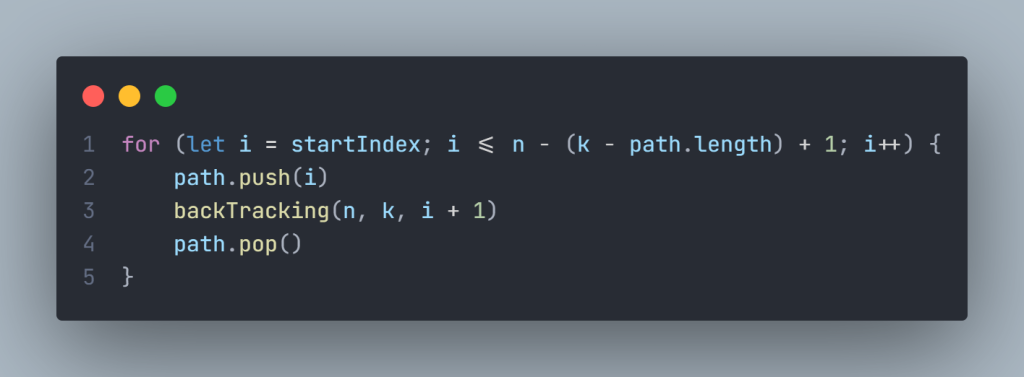
//[ [ 1, 2 ], [ 1, 3 ], [ 1, 4 ], [ 2, 3 ], [ 2, 4 ], [ 3, 4 ] ]剪枝优化
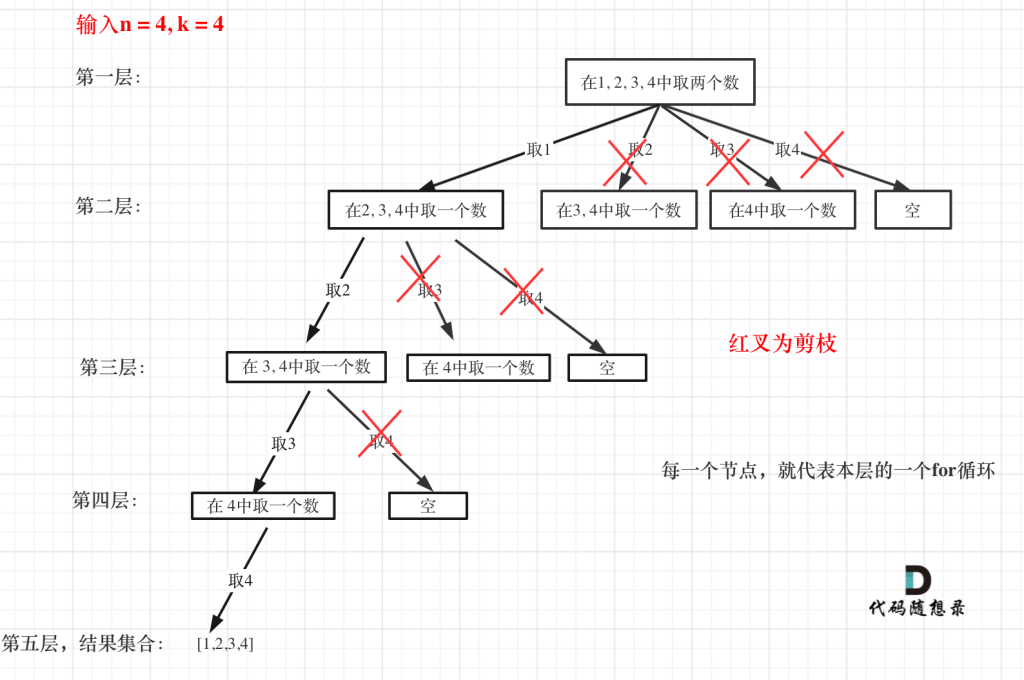
所以,可以剪枝的地方就在递归中每一层的for循环所选择的起始位置
如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索了
- 已经选择的元素个数:path.size();
- 所需需要的元素个数为: k – path.size();
- 列表中剩余元素(n-i) >= 所需需要的元素个数(k – path.size())
- 在集合n中至多要从该起始位置 : i <= n – (k – path.size()) + 1,开始遍历
为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合